ホーム メニュー ![]() 熱と仕事 気体の法則 気体分子運動論 内部エネルギー 気体の状態変化 不可逆変化
熱と仕事 気体の法則 気体分子運動論 内部エネルギー 気体の状態変化 不可逆変化
熱サイクル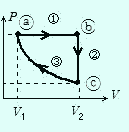
右図で①は定圧変化,②は定積変化,③は等温変化である。
a→b→c→aと連続して変化させる場合,始点と終点はa点だから1サイクル間の温度変化⊿T=0,よって⊿U=0である。
気体に出入りした熱量の総和ΣQ,気体がした仕事の総和ΣW ' の関係は,熱力学第1法則から
Σ(⊿U)=ΣQ−ΣW '=0 ∴ ΣQ=ΣW '
右図の例で過程①は吸熱,②は放熱,③は放熱である。
(過程③でcからa に圧縮すると温度が上昇するので,気体が放熱した結果,等温になることに注意)
また,気体のした仕事は過程①では正,②では0,過程③では負であるが (それぞれの大きさはPV グラフ下の面積である。
12-6気体のする仕事参照),その和ΣW ' は過程①のPVグラフの面積の方が過程③より大きいことから,正である。
よって
ΣQ=ΣW '>0
1サイクルがPV グラフで右回りの場合,気体は吸熱(ΣQ>0),気体のした仕事は正である。
熱機関の熱効率は,
「1サイクルの間に行った正味の仕事の,吸収した熱量に対する割合」と定義される。
正味の仕事とは,PVグラフの面積で,吸収した熱量とは上記の例では,過程①のQの値である。
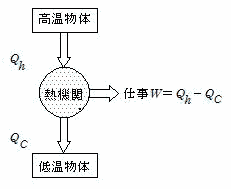
正味の仕事をW,気体が吸収した熱量の和をQh,気体が放出した熱量をQCとすると,熱効率eは
熱効率は,蒸気機関で20%,ガソリン機関で20〜30%,ディーゼル機関で40%位である。
 12−7 熱力学第2法則
12−7 熱力学第2法則
熱に関する現象で,「高温物体から低温物体に向かって熱が流れるが,その逆の流れはない」
「物体が摩擦熱が発生して止まることはあっても,物体が熱を吸収して動き出しことはない」
などがある。これらをまとめたものが,熱力学第2法則である。
クラジウスの原理 「熱は低温部から高温部へひとりでに移動しない」
トムソン(=ケルビン) の原理 「熱はひとりでに力学的仕事に変わらない」
平たくいえば,「与えた熱をまったく捨てずに仕事に変えられない」ということである。
熱に関する現象はいずれも,もとに戻すことができない。一つの現象を,ビデオで撮影しこれを逆回しして同じ現象が起こるものを可逆変化,そうでないものを不可逆変化という。
不可逆変化の例としては,
高・低温度物体の接触または混合、インクなどの水への拡散、摩擦による発熱、熱伝導,気体の自由膨張などがあるが,熱に関わる現象はいずれも不可逆変化である。
可逆変化の例としては,熱現象の伴わない力学,電磁現象,準静的熱現象など数少ない。
12-2 理想気体の巨視的振る舞い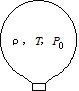
問85 気体の圧力P,密度ρ,絶対温度Tの間に=一定が成り立つことを導け。
問86 熱気球は、バーナーで暖めた空気を気球内に送り込み,浮力で空中に浮上させる装置である。質量がM,体積がVの気球がある。まわりの大気の圧力がP0,気温がT0,密度がρ0であるとき、熱気球を浮上させるには,気球内の空気の温度Tをいくら以上にすればよいか。 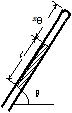
問87 細いガラス管の中に水銀を入れた。ガラス管を水平にした場合(図の角度θ=0),ガラス管内の空気の長さはxθ=5.0cmで,水銀の長さl=20cm,大気圧p0=76mmHgとする。任意の角度θ の場合のガラス管内の空気の長さはxθはいくらになるか。また,θ=90゚の場合の長さはいくらか。温度は一定とする。
12-3 気体分子運動
問88 図に示すように,中心をOとする半径aの球形容器中に質量mの単原子分子からなる1mol の理想気体が入っている。気体分子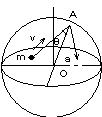 は容器の壁と完全弾性衝突をし,分子どうしの衝突はなく,分子の速さは一様にvであるものとし,重力の影響は考えなくてよい。
は容器の壁と完全弾性衝突をし,分子どうしの衝突はなく,分子の速さは一様にvであるものとし,重力の影響は考えなくてよい。
(1) 図のように,1個の気体分子がA点において入射角θ で器壁に衝突して反射するときに
(a) この気体分子について,運動量変化⊿pを求めよ。
(b) この気体分子がA点で反射した後,再び器壁と衝突するまでに要する時間t0を求めよ。
(c) 単位時間当たりの衝突回数nを求めよ。
(d) 作用反作用の法則によって,この分子から器壁は大きさfの力を受けている。この力をv,m,aで表せ。
(2) (a) アボガドロ数をN として,容器の中にあるN個の分子から器壁が受ける力の大きさF をv,N,m,aで表せ。
(b) この気体の圧力と体積の積pV をv,N,mで表せ。
(c) 理想気体の状態方程式を用いて,全気体分子の運動エネルギーを気体の温度T と気体定数R で表せ。
12-4 分子の平均運動エネルギーと絶対温度
問89 気体分子は熱エネルギーで運動し,絶えず衝突を繰り返している。1個の分子が他の分子と衝突してから,次の衝突までに動いた距離の平均を平均自由行程という。この平均自由行程を次の手順で求める。[
]をうめよ。
いま,分子は直径Dの球とし,弾性衝突をするものとする。さらにすべての分子が動いている状態を考えるのは複雑なので,1個の分子のみ一定の速さvで動き,他の分子は空間に静止して,衝突しても動かないものとする。2個の分子が衝突するためには,互いに分子の中心間の距離が[(1)]にまで接近しなければならない。そこで,動いている分子の半径を(1)の値と同じとすれば,他の分子は点として空間に静止しているものと考えることができる。動いている分子が時間t の間に通過する体積は[(2)]であり,その中のすべての点(分子)と衝突することになる。すなわち分子の密度をnとすれば,単位時間あたりの衝突回数は(3)]となる。したがって平均自由行程は,[(4)]となる。すべての分子が動き回るとして正確に計算した平均自由行程は,(4)の値の![]() 倍になる。
倍になる。
さて,ここで気体を円筒容器にいれた後,ピストンを動かし,温度を一定に保って,気体に圧力をK倍にしたときの様子を調べよう。このとき,気体の体積は[(5)]倍,気体分子の密度は[(6)]倍,2乗平均速度は[(7)]倍なる。したがって,平均自由行程は[(8)]倍になる。
12-6 熱力学第1法則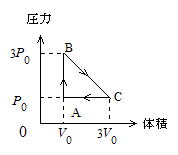
問90 単原子分子からなる1モルの理想気体の体積と圧力を図に示すように,A→B→C→Aの経路にそって変化させた。
Aでは体積,圧力および温度がそれぞれV0,P0,T0,またBでは圧力が3P0,Cでは体積が3V0であった。A→Bでは体積一定,B→Cでは圧力,体積の関係を直線的に,C→Aでは圧力一定のもとに変化させた。気体定数をRとする。
(1) (イ) Bでの温度 (ロ) Cでの温度はいくらか。
(2) A→Bの過程で気体が外部から吸収した熱量はいくらか。
(3) B→Cの過程では外部との間で熱の出入りが認められた。BからCに到達したときどれだけの熱を吸収したか。
(4) C→Aの過程で気体が外部に放出した熱量はいくらか。
(5) B→Cの過程での温度−体積の関係を示すグラフを描け。
問91 理想気体1molを、図1のようにシリンダー・ピストン系に閉じこめ、適当に加熱または冷却し、ピストン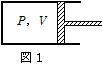 をなめらかに移動させる。気体の圧力をP,体積をVとし,図2のような状態をA→B→C→Aに変化させた。A→B過程は断熱変化である。3つの過程A→B,B→C,C→Aについて,気体の内部エネルギーの変化⊿U(増加を正とする),気体に出入りする熱Q(気体に入る場合を正とする),気体がするまたはされる仕事W(気体がピストンにする仕事を負とする)を,状態A,Bの圧力および体積つまりP1,P2,V1,V2,気体の定積モル比熱CV,気体定数Rを用いて表せ。⊿U,W,Qについて符号をつけて答えよ。
をなめらかに移動させる。気体の圧力をP,体積をVとし,図2のような状態をA→B→C→Aに変化させた。A→B過程は断熱変化である。3つの過程A→B,B→C,C→Aについて,気体の内部エネルギーの変化⊿U(増加を正とする),気体に出入りする熱Q(気体に入る場合を正とする),気体がするまたはされる仕事W(気体がピストンにする仕事を負とする)を,状態A,Bの圧力および体積つまりP1,P2,V1,V2,気体の定積モル比熱CV,気体定数Rを用いて表せ。⊿U,W,Qについて符号をつけて答えよ。
12-7 熱力学第2法則
問92 密閉された室内で大型の冷蔵庫が運転されている。室内の人間は熱く感じたので冷蔵庫の扉を開けていけば少しでも涼しくなると思い,冷蔵庫の扉を開けた。十分な時間が経過した後,扉を閉じたままの状態および冷蔵庫を運転していない状態と比較して室内の温度はどうなるか。理由をつけて答えよ。
ホーム メニュー 熱と仕事 気体の法則 気体分子運動論 内部エネルギー 気体の状態変化 不可逆変化
Top