�z�[�� ���j���[ ![]() �M�Ǝd�� �C�̖̂@�� �C�̕��q�^���_ �����G�l���M�[ �C�̂̏�ԕω� �s�t�ω�
�M�Ǝd�� �C�̖̂@�� �C�̕��q�^���_ �����G�l���M�[ �C�̂̏�ԕω� �s�t�ω�
�P�Q�|�Q ���z�C�̂̋����I�U�镑��
�C�̂̈���
�P�ʑ̐ς�����̖ʂɐ����ɓ����͂����͂Ƃ����B
�ʐ�S[m2]�̖ʂɗ�F[N]�������Ƃ��C����P[N/m2]���ƒ�߂�B�P�ʂ� [N/m2]�����CSI�P�ʌn�ł�1[Pa�p�X�J��]��1[N/m2] �Ƃ���B
�P�C����76cmHg��0.76m�~1m2�~13.59�~103Kg/m3�~9.807m/s2�^1m2��1.013�~105Pa
�@�@�C�̂��~�N���̗���ň���P[Pa]�C�̐�V[m3]�C��Ή��xT[K]�̊Ԃɐ��藧�W���͈ȉ��̒ʂ�B
1�C���ł�1m2�������104KgW��10tonW�ł���C����͍L�����V���ɖ�10tonW�̗͂������Ă���I
 �@�@�{�C���̖@��(R.Boyle1627-1691)
�@�@�{�C���̖@��(R.Boyle1627-1691)
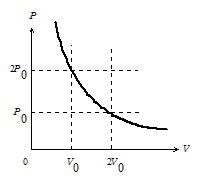
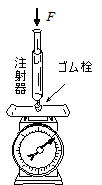
��Ή��xT�����̂��ƂʼnE��}�̂悤�ɋ�C�����ăS�������������ˊ������̏�ɍڂ��C��Ő����ɂ������͂�������B��̗͂̑傫��������̖ڐ��肩��ǂ݁C�����ɂ��̂Ƃ��̒��ˊ���̋�C�̑̐ς𑪒肷��B�c���Ɉ���P����F�^(���ˊ�̒f�ʐ�)�C�����ɑ̐ςɂƂ��ăO���t��`���Ɛ}�̂悤�ɂȂ�B���̂��Ƃ���
�u���x�����̂Ƃ��C��莿�ʂ̋C�̂̑̐�V�͈���P�ɔ���Ⴗ���v
PV����� ������{�C���̖@���Ƃ����B
�{�C���̖@����1662�N�ɔ������ꂽ���C1676�NE.Matriot���ڂ����������BMatriot(�}���I�b�g)�͖ڂ̖ӓ_�����Ă���
�@�@
�V�������̖@��J.A.C.Charles1746-1823)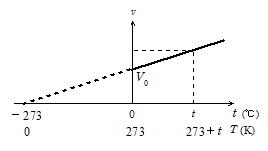
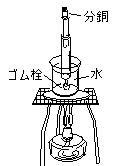
�E�}�̂悤�ɐ����ɗ��Ă��S����t�����ˊ�𐅑��ɓ���C��[�ɕ������ڂ���B�����͎��R�ɓ�����̂ň��͂����ƍl������B
���������M���C���������x�C�c���𒍎ˊ���̋�C�̑̐ςɂƂ��ĉE�̃O���t�����B
�@���xt��0(��)�̑̐ς�V0�C���xt�̂Ƃ��̑̐ς�V�C��Ή��x��T(K)��273�{t(��)�Ƃ���ƁC�O���t�̌X������(�C�̂̎�ނɂ�炸���l)�C�����莮�������
�@�@�@��
�u���͈��̂Ƃ��C�C�̂̑̐ςƐ�Ή��x�͔�Ⴗ��v ������V�������̖@���Ƃ����B
�V�������̖@����1787�N�������ꂽ��1802�N�Q�C�����T�b�N�����������������̂ŃQ�C�����T�b�N�̖@���Ƃ��Ă��B�Q�C�����T�b�N��1804�N�C����7000m���ő�C�����C�n���C�������B1808�N�C�̖̂@�������B
�V�������̖@���ɂ��Ɛ��0�x�ő̐�V��0�ɂȂ邪�C�C�̂͒ቷ�ɂȂ�Ɖt�́C�ő̂ɏ�ԕω����邩��0(K)�̋C�̂͑��݂��Ȃ��B
�{�C���V�������̖@��
�{�C���̖@���ƃV�������̖@�����ɕ\�������̂��{�C���V�������̖@���ł���B
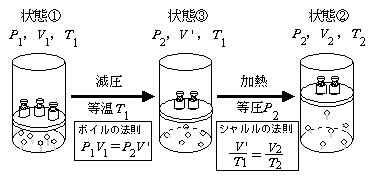
�㍶�}�ŁC��ԂP(�O���t�@)��P1�CV1�CT1�C���ԏ�Ԃ�(�O���t�B)P2�CV '�CT1�C��ԂQ(�O���t�A)��
P2�CV2�CT2 �ł���B
��ԂP�ƒ��ԏ�Ԃ̊ԂŃ{�C���̖@��P1V1��P2V ' (�@�ƇB�̊Ԃ�P ��V �ň͂܂ꂽ�����̖ʐς����)�C
���ԏ�ԂƏ�ԂQ�̊ԂŃV�������̖@���̊W�����藧�B�������� V ' �����������
(�{�C���E�V�������̖@��)
�����藧�B
�{�C���V�������̖@���͈��͂����������C���x���Ⴗ���Ȃ��͈͂ł��ׂĂ̋C�̂ɓK���ł��邪�C���藧�͂ɂ͋C�̂̎�ނɂ���ĈقȂ�B�t�����ɂ���H2�CO2�CN2���Ȃ�L���͈͂Ő��藧���CCO2�͍ł��K���������BHe���ł��K���͈͂��L���B
���z�C��(ideal gas)�̏�ԕ�����(equation of state)
�u1mol�̋C�̂́C�C�̂̎�ނɊW�Ȃ��C�W����Ԃłق�22.4l �̑̐ς��߂�v ���Ƃ���C1mol�̕W����Ԃ̋C�̂ɂ��āC�{�C���E�V�������̖@����P��1.013�~105Pa�CV��22.4�~10�|3m3��������
R��
����R ���C�̒萔�Ƃ����B1mol �ɂ���PV��RT
������n �ł͑̐ς�n �{�ɂȂ邩��
�@�@�@PV��nRT
���݂̋C�̂ł͌����ɂ͂��̊W���͐��藧���Ȃ��B�{�C���E�V�������̖@�������藧�C�̂𗝑z�C�̂Ƃ����B����Ă��̊W�������z�C�̂̏�ԕ������Ƃ����B���݂̋C�̂ł́C���q�Ԃ̈ʒu�G�l���M�[�������ł���͈́C�܂荂���C�ሳ�̏�Ԃ����z�C�̂ɋ߂���Ԃł���B�ȍ~�͗��z�C�̂ɂ��čl����B�@
����100���C1atm�Ő����C�ɂȂ�ƁC�̐ς͖�1700�{�ɂȂ�B�����̂̊e���_�ɐ����q���z�u����Ă���Ƃ��C�����C�ɂȂ����Ƃ��ĕӂ̒�����n�{�ɂȂ����Ƃ����
n3��1700����n��11�D9�{�ł���B�C�̂Ɉ��k��������̂́C�C�̂̕��q�ԋ������ő́C�t�̂ɔ�ׂđ傫�����߂ł���B
1l ��(10cm)3��10-3m3 22.4l ��22.4�~10-3��2.24�~10-2m3���m�ɂ�22.41383 l
�W����Ԃ�0����273K 1�C��(atm)��1.013�~105Pa
��1 T��0���CP��1atm,V��1l �̋C�̂���ꂽ�e�킪����B
�@�@�@(1) ���͂����ɂ���t '��100���ɂ����B�̐�V '��V�̉��{�ɂȂ邩
�@�@�@(2) �̐ς����ɂ���t '��100���ɂ����B����p '��p �̉��{�ɂȂ������B
�� (1)�{
�@ (2)
��2 �[��10m�̐���(������5��)�ɂ������̐�V1�̋C�A�͐��ʏ�ʼn��{�ɂȂ邩�B�������C���ʂł̉��xt2��27���C��C��P2��1atm�Ƃ���B�܂��C���[��1.0m����0.10atm���͂������Ȃ�Ƃ���B
�� �[��10m�ł̈��͂�P1�C���x��T1�C���ʂł̑̐ς�V2���x��T2�Ƃ���ƁC�{�C���E�V�������̖@������
�{
��3 3.2mg�̃��^��(���q��16)�̑̐�V��20cm3��27���̂Ƃ��̈���P�͂����炩�B
�� 3.2(mg)�Fn (mol)��16(g)�F1(mol) ��
�@�@
��4 ���`�̗e��A�CB�ɂ��ꂼ�̈��́C���x�C�����ʂ�PA��1atm�CTA��273K�CnA mol�CPB��2.5atm�CTB��343K�CnB mol�̋C�̂�����Ă���C�R�b�N�Ŏd���Ă���B�̐�Vm3�͓����ł���B�R�b�N���J������̈���P�����炩�B�������R�b�N���J����������x��A�CB�Ƃ��ɃR�b�N���J���O�Ɠ����Ƃ���B
�� �R�b�N���J�������A�CB���ꂼ��̕����ʂ�nA'�CnB'�Ƃ���ƁC�����ʂ͕ۑ�����Ă��邩��
nA�{nB��nA'�{nB'
�R�b�N���J���O��ŋC�̂̏�ԕ�������K�p����
�@�@�@�@�@A�F1�~V��nAR�~273�C2.5V��nBR�~343
�@�@�@�@�@B�FPV��nA'R�~273�CPV��nB'R�~343
�@�@�������
�@�@�@�@�@�@
�z�[�� ���j���[ �M�Ǝd�� �C�̖̂@�� �C�̕��q�^���_ �����G�l���M�[ �C�̂̏�ԕω� �s�t�ω�
Top