�z�[�� ���j���[ ![]() �d�q�ƌ� �g�����Ɨ��q�� ���q�\�� ���q�j �j����j�Z�� �N�H�[�N
�d�q�ƌ� �g�����Ɨ��q�� ���q�\�� ���q�j �j����j�Z�� �N�H�[�N
�y�Q�R�z���q�\��
�P.���f���q�̃X�y�N�g��(spectrum)
1884�N�o���}�[�̎����ɂ���Đ��f���q�̔�����X�y�N�g�������肳�ꂽ�B�������Ƃ��ĂS��ނ̔g��������ł����B���ꂼ��̔g��
H���CH���CH���CH�� �̒莮���͎��̒ʂ�B
�~B (B��3645.6��)
H����6563�� (9/5) �� 32/5 �� 32/(32�|4)
H����4861 (4/3) �� 42/12 �� 42/(42�|4)
H����4340 (25/21) �� 52/21 �� 52/(52�|4)
H����4102 (9/8) �� 62/32 �� 62/(62�|4)
����炩��g�����ȉ��̂悤�ɒ莮�������B
(n��3�C4�C5�C6)
���̌ナ���[�h�x��(1854-1919)�̒��������[�h�x���萔R��1.097�~107(1/m) ��p����
�Ə���������ꂽ�B���f���q�̃X�y�N�g���́C�͂��߃o���}�[�ɂ���ĉ��㕔�����肳��C��Ɏ��O�����C�ԊO�����̂��낢��ȃO���[�v�����肳�ꂽ�B�����̃X�y�N�g���̃O���[�v���n��(series)�ƌĂԁB
1906�N ���C�}���n��(n��2�C3�C4�C5) (���O��)
1908�N �p�b�b�V�F���n��(n��4�C5�C6�C7) (�ԊO��)
�Ȃǂł��邪�C�E�ӑ�P���̕���̐�(���L��m)�ɂ����
�P�����C�}��(Lyman 1906)�n��C�Q���o���}�[(Balmedr 1884)�n��C�R��(���b�c�)�p�b�V�F��(Paschen 1908)�n��C
�S���u���P�b�g(Brackett 1922)�n��C�T���v���g(Pund 1924)�n��
�Ɩ��t�����Ă���B ( )���͔������ꂽ�N�ł���B
��������ʉ������
(n��m�{1�Cm�{2�Cm�{3�C���) (23-1)
���f�^�C�I���C���̑��̌n��
���f�^�C�I��
(m��2 Lyman�Cm��3 Fowlar�Cm��4 Pickering �n��)
(m��6 Nicholson�n��)
���̑�
m�������C��s�C��p(��1)�͊e�n��ŗL�̒萔
�Q.���q�͌^(atomic model)
���q�͌^�ɂ��Ĉȉ��̑�\�I�Ȗ͌^���l����ꂽ�B
(1) �g���\��(J.J.Thomson 1856-1940)���f��(1903�N �����Ԃǂ�����P�[�L(plum pudding)�^)
�L�����ɕ��z�������ɓd�q�����}�̂悤�ɕ��z����B
���̃��f���ł́C���q������ł���B����̂��߂ɓ����̓d�q�z�u�Ɏ����I�ɓ����p�^�[��������C���f�̎�����������B
�d�q�������̌����ł荇���ʒu����O���ƁC�d�q�͂��̈ʒu�̂܂��ɐU������B�������āC���q��������ˏo�����B
���̌��̐U���������ʊϑ�����錴�q�X�y�N�g���̒��x�̑傫���������߂ɕK�v�Ȑ��d�ׂ̋��̑傫���̌v�Z���炨�悻10-10m�ł������B
(2) ����(1865-1950)���f��(1903�N)
���̓d�ׂ��W�����C�܂��ɓd�q���y���̊̂悤�ɕ��z����B���̔z�u���͊w�I�Ɉ��肵�Ă���Ƃ������C�d�q���Î~���Ă��Ȃ��̂ŁC�}�b�N�X�E�G���̗��_����l����ƁC�����ˏo����̂ň���ł͂Ȃ��B���q�̑傫����10-10m�ł��邱�Ƃւ̕K�R���̐������s���ł���B
�{���c�}���̒�q�ł��钷���̓}�b�N�X�E�G���̗͊w���f������l�������C���N���q�̌`���ߒ��ɂ��āC�J���g�̐��_���ɂ��f���̌`���ߒ������Ƃɘ_���Ă���B
�ԊO���X�y�N�g���͗z�d�ׂ̐U���ɑΉ��C�уX�y�N�g���͋O���ʂɐ����ȓd�q�̐U���ƑΉ�����Ƃ����B
(3) ���U�t�H�[�h(1871-1937)���f��(1911�N)
���d�ׂƎ��ʂ����S�ɏW��������߂ď������j�����C���̂܂��𐳓d�ׂz�Ƃ���ƁC�d�q���f���̂悤�ɂ܂��B
1909�N�C��q�K�C�K�[(H.Geiger1882-1945)�C�}���X�f��(E.Marsden)�̋������g������ ���U�������ɂ���āC���d�ׂ̏W������10-15�`10-14m�̕������j�Ɩ��Â����B���q�ԍ�z�̌��q�́C�{z e�̐��C���̂܂���z�̓d�q����Ȃ�Ƃ����B
�U�������̌����R.�{�[�A���q���f�� (1913�N)
�@ ���q���ŁC8000�̓����� ���ɑ���1�̊����ł��̎U�����N����B�܂�C�g���\�����f��(�L���d�ׂ����z����)�͕s�K�ł���B
�A ���d�ׂ�_�d�ׂƂ���ƁC�U������������ꑪ�茋�ʂƂ悭��v�����B
�B ��ʂɌ��q�ԍ�z e �̓d�ׂ����B(z �����q�ԍ��Ƃ��邱�Ƃ̓u���b�N(A.V.d.Broek)�ɂ��)
���U�t�H�[�h���f���̍���_
�@ ���������ɂ���Č��q�̑傫�������߂���͂��ł���B���錴�q�����̃X�y�N�g���C�G�l���M�[�������Ƃ��s�\�ŁC�j�̎��ʂ��d�q�̎��ʂ��\���傫���j���Î~���Ă���Ƃ����Ƃ��C���̓d�ׁ|e�Ǝ��ʂ����ő傫�������������̎����ɂȂ�Ȃ��B
�A �d�q�̋O�������܂��Ă��C(�}�b�N�X�E�G���̗��_����)���q�͉~�^������Ƃ��ɓd���g���o���C�G�l���M�[�������ēd�q�͊j�Ɉ���������͂��ł���B(���f�̏ꍇ�C1.6�~10�|11�b�ŏ��ł���)
�B ���q�̔�����X�y�N�g����
�����͋O�����ar���������Ȃ�Ə������Ȃ�C���̐U�����͈��łȂ��B���f�����̃X�y�N�g�����o�����Ƃ̐������ł��Ȃ��B
���U�t�H�[�h���f���ɑ��鍢����������邽�߂ɁC�{�[�A�͈ȉ��̂悤�ȂQ�̑�_�Ȍ��q���f�����l�����B���̍ő�̓����̓v�����N�萔���g�������ƂƁC���q�̃G�l���M�[�����U�I�ł���ƍl�������Ƃɂ���B(1)�̗ʎq�������l���邽�߂ɁC����(�p�^����)�ƈ�v����E�ӂ��l�������C�ÓT�����w�ł͉����ł��Ȃ��������߂Ƀv�����萔�������Ƃ����B
(1) �ʎq����
���q������Ԃł́C���q�͓d���g���o���Ȃ��B�����̏ꍇ��������Ԃ��\�ł���B
mvr��n() (23-2)
������m�Cv�C r �͂��ꂼ��d�q�̎��ʁC���x�C�O�����a�Cn�͗ʎq���ł���B
���̏�������C����Ԃł̃G�l���M�[En�͂ƂтƂ�(���U�I)�ɂȂ�B
�� (23-2)������������ 2��r��n() �ƂȂ�C���ӂ͔��ar�ł̉~�����C�E�ӂ�
�̓h��u���C�̕����g�̔g��������C
�u�d�q�̋O�����a�������g�̐����{�̏ꍇ��������Ԃ����݂���v�Ƃ�����B�������C�h��u���C�������g������̂�1923�N������{�[�A���_�̕������j�I�ɂ͐�ł���B
(2) �U��������
���q���G�l���M�[����En����En' (En��En' �Ƃ���)�̒���ԂɈڂ�Ƃ�(�J�ڂ���Ƃ�)�CEn�|En' ��h�˂̃G�l���M�[�̌��q����o(�z��)����B
En����En' �ɑJ�ڂ���ꍇ�͌��q����o���CEn' ����En�ɑJ�ڂ���ꍇ�͌��q���z������(�G�l���M�[���K�v�Ƃ���)
�����̉��肩��O�����ar �ƃG�l���M�[En�����߂�B
�O�����ar
�d�q(����m�C�d�ׁ|e)���Î~���Ă���j(�d��+e)�̂܂��𑬂�v�œ����~�^�����Ă���ƁC�N�[�����͂����S�͂ɂȂ邩��~�^���̉^������������
��������@
�ʎq��������
mvr��n() ��
����A
�@���A����
��� �B (23-3)
�� n��1��r��0.53�~10-10m(������{�[�A���a�Ƃ���)�ɂȂ�B���̑傫���̓��U�t�H�[�h�� ���U�������̌��ʂƈ�v����B
�G�l���M�[En
�^���G�l���M�[�ƈʒu�G�l���M�[����G�l���M�[�����߂��
En��(n��1�C2�C3�C���) (23-4)
�� ���̎�����킩�邱�Ƃ́Cn��1�̏ꍇ(���������ԂƂ���)�̋O�����a�ɑ��āCn��2�C3�C4�C����̋O�����a��4�{�C9�{�C16�{�ɂȂ�C�~�O������������Ȃ����ƂɂȂ�B���̂��Ƃ͌��q�ԍ����傫�����̂ɂ��đΉ��ł��Ȃ����ƁC���ׂĂ̌��q�̔�����X�y�N�g��������ł��Ȃ����ƂȂǂ̕s�\����������B��������������̂��C�ȉ��Ɏ����]���}�[�t�F���g�ɂ�闝�_�ł���B
�{�[�A���_�̎����ł̗��t��
�{�[�A���_���Ó��Ȃ��̂��ۂ��͎����ŏؖ�����Ȃ���Ȃ�Ȃ��B�ȉ��̂Q����\�I�Ȏ����I�ؖ��ł���B
�@ �X�y�N�g���Ƃ̑Δ�
(23-4) ��ʎq��n�Cn' �ɂ��čl�����
En�|En'��h�ˁ�hc/��
�@�@�@�@ ��
���̎��̓o���}�[�n��͂��܂������f�̃X�y�N�g���̒莮���� (23-1) �Ɠ����`�����Ă���B
�������ƃ����[�h�x���萔R���ׂ�� R��1.10�~107(1/m)�Ɠ������B
�@�@�@�@n' �����Ƃ����
�@�@�@
�Ə������Ƃ��ł���B
�@�� �E�}�̐���(�G�l���M�[���ʂƃX�y�N�g��)
���f���q�̃G�l���M�[���ʂ��E�}�Ɏ����B�ł��G�l���M�[���������̂�����Ԃł��邱�Ƃɒ��ӁB
(23-1) �ƑΔ䂷��Ƃ킩�邪�C�G�l���M�[���傫����Ԃ���
m��1�֑J�ڂ���ꍇ�����C�}���n��C
m��2�֑J�ڂ���ꍇ���o���}�[�n��(�������͂S��ނ̂�)
m��3�֑J�ڂ���ꍇ��(���b�c�)�p�b�V�F���n��C
�@m��4�֑J�ڂ���ꍇ���u���P�b�g�n��
m��5�֑J�ڂ���ꍇ���v���g�n��
�ł���B���̂��Ƃ���C���q����o���ꂽ���̔g�����킩��C�ǂ̏�Ԃ���ǂ̏�ԂɑJ�ڂ��������킩��B
��P ���f�̏ꍇ�C�ł���B
(1) n��3����n��2�ɑJ�ڂ����B�G�l���M�[����
(2) ���̂Ƃ��ɏo�Ă�����̐U�����˂́C�g���ɂ�
��
��
��Q ���f���q�� n���P(�����)�ɂ���(E���|13.6eV)�B�����10.2eV�̌��q�Ă�B�ǂ̂悤�ȏ�Ԃ��B
�@�@�@�@�@�@�|13.6�{10.2���|3.4eV �� n��2
�A �t�����N��w���c�̎���
���f�������X�y�N�g���̔g�����@����悭��v���邱�Ƃ��킩�������C���q�̃G�l���M�[�����U�I(�ƂтƂ�)�ł��邱�Ƃ͏ؖ�����ĂȂ��B���̂��Ƃ��{�[�A���_�����\���ꂽ���N�C�����ɂ���ďؖ������̂��t�����N(J.Frank
1882-1964)��w���c(Gustav.Herz1887-1950)�̎����ł���B
(�w���c�͐U�����̒P�ʂɂȂ��Ă���Heinrich.Rudolph.Herz1857-1894�Ƃ͕ʐl�ł���)
������C�����߂��e��ɉ��}�̂悤�Ƀt�B�������g��M���ĔM�d�q��������B�d��P�͗z�ɂł���CG��P���0.5V�����d�ʂ��������Ă���BF���o�Ă����d�q�͗z��P�Ɍ������Đi�ށB���⌴�q���W���Ȃ��Ȃ��H�ɗ����d���͒P����������͂������C�����ɂ���4.9V�Ԋu�œd�����������J��Ԃ��B�d������������͓̂d�q��P�ɒB����O�ɐ��⌴�q�ɂ���ăG�l���M�[��D����ƍl������B���⌴�q������Ԃ������N��ԂɑJ�ڂ��邽�߂ɃG�l���M�[��D���ƍl����ƁC���̎������ʂ�������邱�Ƃ��ł���B
�d�q�̃G�l���M�[��V(eV)������CV����E(��4.9eV)�̏ꍇ�ɐ��⌴�q�͓d�q����G�l���M�[��D�킸V����E�̏ꍇ�ɓd�q�͐��⌴�q����G�l���M�[��D���B�����āCG�̓d�ʂ�P���0.5V��������CV�|��E��0.5�ł�P�ɒB���邱�Ƃ͂Ȃ��C0.5��V����E��P�ɒB���邱�Ƃ��ł���B�����̂��Ƃ��琅�⌴�q�����U�I�ȃG�l���M�[�������Ă��邱�Ƃ��ؖ����ꂽ�B�X�ɃG�l���M�[���ʂ��������(��P��N��Ԃ������Ԃւ̑J��)�G�l���M�[�̍��ɓ�����������o���邪(�{�[�A���_�A�U��������)�C4.9eV�ɑ���������̔g���ɂ�
![]()
���̌��͎��O���ł���C���ۂɊϑ����ꂽ�l�ƈ�v���Ă���B���̂��Ƃ���U�������������藧���ƁC���q�̃G�l���M�[�����U�I�ł��邱�ƁC�܂�ʎq�������ؖ����ꂽ�B
�@�����Œ��ӂ�v����̂́C4.9eV�̂Q�C�R�{�œd�����������͂��߂�̂͑�Q�C��R��N��ԂɑJ�ڂ��邽�߂ł͂Ȃ��Ƃ������Ƃł���B�������̍l�����������Ȃ�G�l���M�[���ʂ͓��Ԋu�ł��邱�ƂɂȂ�C���₪������X�y�N�g���̌o�����Ɩ�������̂Ő������Ȃ��B�ł͂Ȃ��s���悭4.9eV�̐����{�ɂȂ��Ă���̂��B����́C����12eV�̃G�l���M�[���������d�q��P�Ɍ������ꍇ���l����ƁC��̐��⌴�q��4.9eV�̃G�l���M�[��D�������ʁC���̓d�q��12�|4.9��7.1eV�̃G�l���M�[�������Ă���B�X�ɕʂ̐��⌴�q�����̓d�q����G�l���M�[��D���āC�d�q�̎c��̃G�l���M�[��7.1�|4.9��1.2eV���c�����ƂɂȂ�C���ꂪGP�Ԃ̓d�ʍ�0.5eV���傫���̂�P�ɒB���邱�Ƃ��ł���B���̂悤�ɍl���邱�Ƃɂ���āC���ꂼ��̐��⌴�q��4.9eV�̃G�l���M�[������d�q����D���Ɛ������邱�Ƃ��ł���B
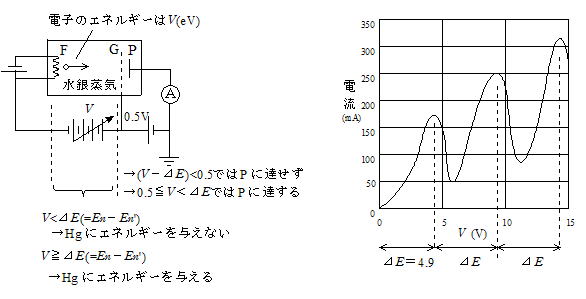
�����Ɏ����ꂽ4.9V�����d��(V)�ƌĂԂ��C���̌��q�ɂ��ĎQ�l�܂łɉ��L�ɋL���B
Hg(4.9)�CK(1.63)�CNa(2.12)�CHe(21)
(���݂�Na��2.12eV�ɑΉ�����g������̎����g���Čv�Z�����5.84�~10-7m�ł��肱��̓i�g���E��D���̔g���ƈ�v����)
�{�[�A���_�͌ÓT�_�ł̖���������������̂��������C�{�[�A���_�ł͉~�O������������Ȃ��Ȃǂ̍���_���������B����ɑ���Sommerferd(1868-1951)��ɂ���ĕ���ꂽ���C����ł��Ȃ����̔g������������C�X�y�N�g�����x�̐������s�\�ł������B���̌�C��ʎq�������������̂ɉ����āC���ʗʎq��(�ȉ~���l����)�C���C�ʎq��(�d�q�̉~�^���̌���)�C�X�s���ʎq��(�d�q�̉�]�ɂ��Ă̗ʎq��)�̂S�ŕ\�����Ƃɂ���Ă��܂��莮�����Ȃ��ꂽ�B���ꂪ�V�����[�f�B���K�[�̔g���������ł���B
(1) ���ʗʎq�� l
�d�q�͋O���^���ɑ���p�^���ʂ������C���̓��a�����C���a�ɐ����ȉ������������C������Ԃ̐ϕ��l�͗ʎq������B
���a�����ʎq��nr�C���ʗʎq��l (n��)�Ƃ����
nr�{n����n (��ʎq��)
���ʗʎq��l(n��)�����d�q�̊p�^���ʂɊW�������C���̊p�^���ʂ�
n��l�ł���B(l��0�C1�C2�C���n�|1��n��)
�C
(2) ���C�ʎq�� m����O���ȉ~�ʂ̌X��������
�d�q���j�̂܂����^������ƁC���C���[�����g��L���鎥�ΔƓ���������C����Ɏ����������ƃ��[���A���^��(���܂̎�U��^���Ɏ���)����B���̂Ƃ��̊p�^���ʂ̉�������������̐����̐������ʎq�������̒l���Ƃ�B
l��m���|l �Ƃ���2n+1�� ���Ƃ�B
(3) �X�s���ʎq�� s
�d�q�̎��]�ɂ��p�^���ʂ������C������ʎq�������B���̒l���̐����{(0���܂ށB������{�[�Y���q�Ƃ���)���������{(�t�F���~���q�Ƃ���)�ł���B�d�q�C�j�q�C�����Ԏq�̃X�s����1/2�C���q�̃X�s����1�C�����Ԏq�̃X�s����0�ł���B
�p�E���̋��������L�̗ʎq��n�Cl�Cm�Cs�Ō��߂���d�q�͂P�������݂������Ȃ��B�t�F���~���q�͂���ɏ]���B
�]�k ����������������������������������������������������������������������������������������������������
�{�[�A���_�������O�ɗF�l�n���Z�����u�o���}�[�̌���������悤�v���߂��Ƃ���C�u������炩�ɂȂ����v�ƌ�����Ƃ����B
�{�[�A���_�ɑ��镨���w�҂̔���
���U�t�H�[�h�F�u�d�q�͎������ǂ��ɔ��ł������m���ĂȂ���Ȃ�Ȃ��v
���C���[�F�u���̐��ɍ���Ȃ��v
���D�G�ƃV���e�����F�u���ꂪ�������ƂȂ����畨���w�҂����߂�v����ł����߂Ȃ������B
�A�C���V���^�C���F�u�ƂĂ��C�ɓ������v
����������������������������������������������������������������������������������������������������������
�y�Q�R�z��� �G�l���M�[�o���h
�C�̏�Ԃ̌��q���œd�q�̃G�l���M�[�́A���̌��q�ɓ��L�ȂƂтƂт̒l�i�G�l���M�[���ʁj���������Ƃ��ł��Ȃ��B����A�����̌��q���W��������Ԃł́A�����̏��ʂ����镝�̒��ɏW�܂邽�߁A�d�q�̃G�l���M�[���ʂ͑я�ɕ��z����B������G�l���M�[��(�G�l���M�[�o���h)�Ƃ����A�тƑт̊Ԃ̃G�l���M�[���ʂ̂Ȃ��������֎~��(�G�l���M�[�M���b�v)�Ƃ����B�G�l���M�[�тł��ЂƂ̃G�l���M�[���ʂɂ͌��܂������̓d�q��������Ȃ��̂ŁC�d�q�͒Ⴂ�G�l���M�[���ʂ��珇�Ԃɋl�܂��Ă����B
�@���́C�s���́C�����̂̈Ⴂ�̓G�l���M�[�тւ̓d�q�̋l�܂���̈Ⴂ�ł���B
�@���̂ł́C�d�q���l�܂��Ă���ł������G�l���M�[�т��d�q�Ŗ�������Ă��炸�C�ЂƂ̃G�l���M�[�т̒��ł͏��ʊԂ̍����������̂ŁC�d�q�͍����G�l���M�[���ʂɗe�ՂɈڂ邱�Ƃ��ł���B���̂��ߓd�q�͎ア�d��ɂ���Ă��e�ՂɈړ��ł��C���ꂪ���R�d�q�ł���B���̂悤�ɁC�����̎�ނł��܂鉽�Ԗڂ��̃G�l���M�[�т̓r���܂œd�q���������G�l���M�[�т�`���тƂ����A���̉��̃G�l���M�[�т͓d�q�ŏ[������Ă���B���̃G�l���M�[�т����d�q��(�܂��͏[����)�Ƃ����B
�����ł͉��x�������Ȃ�ƌ��q�̔M�U�����������Ȃ莩�R�d�q�̉^�����W�����d�q������ɂ����Ȃ��R���͑�������B
�s�����ł͉��Ԗڂ��̉��d�q�т܂ł��d�q�Ŗ�������C�֎~�т̏�̓`���тɂ͓d�q���Ȃ��B���q�̌����̂��߂ɓd�q���g���C�]���ȓd�q���Ȃ����߂ł���B
�^��������(Si�CGe)�ł́C�[���тƓ`���т̊Ԃ̋֎~�т̕�����r�I�������̂ŁC�M�^���ɂ���ēd�q���`���тɏオ���ēd�q���Ăяo�����オ�z�[���ɂȂ�B
�@�����̂ł͉��x�������Ȃ�Ɠ`���тɏオ��d�q������������̂œd��������₷���Ȃ��R���͌�������B
�s����������
p �^�����̂ł͉��d�q�т̂�����ɁC(B�CAl�AIn) �Ȃǂ̃A�N�Z�v�^�[�ɂ�鏀�ʂ�����̂ŃL�����A��e�Ղɐ����邱�Ƃ��ł���B
n �^�����̂ł͓`���т̂������� (P�AAs�ASb) �Ȃǂ̃h�i�[�ɂ�鏀�ʂ�����̂ŃL�����A��e�Ղɐ����邱�Ƃ��ł���B
�z�[�� ���j���[ �d�q�ƌ� �g�����Ɨ��q�� ���q�\�� ���q�j �j����j�Z�� �N�H�[�N