ホーム メニュー ![]() 静電界 コンデンサー 直流回路 磁界 電磁誘導 交流
静電界 コンデンサー 直流回路 磁界 電磁誘導 交流
【20】電磁誘導(electromagnetic induction)と交流(alternating current)
20-1 電磁誘導の法則
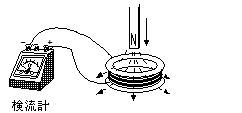
図のようにコイルに検流計をつなぎ磁石を近づけたり遠ざけたりすると,コイルに電流が流れることが観察できる。これは,コイルを貫く磁束が時間に対して変化することが原因である。このような現象を電磁誘導といい,生じる起電力を誘導起電力,流れる電流を誘導電流という。
ファラデーの電磁誘導の法則
「コイルに生じる誘導起電力Vは,コイルを貫く磁束φの単位時間当たりの変化に比例する」
コイルの巻き数をn とすると
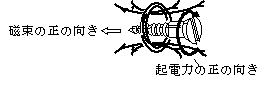
(20-1)
磁束:磁界の中で磁界に垂直な面の断面積S[m2]と,磁束密度 B[T]の積 φ=BS をその面を通る磁束という。磁束の単位はWb(ウエーバー)である。
磁束,誘導起電力の符号は次の約束をする。コイル面と垂直に右ねじを立てたとき,ねじの進む向きにコイルを貫く磁束を正の磁束,ねじをまわす向きに発生する誘導起電力を正の起電力とする。
(20-1)式の負号は,コイルを貫く磁束変化が正のとき,誘導起電力が負の向きに発生することを意味している。
閉曲面で囲まれた全面積SをBが一定と見なせる微小面積⊿Siに分割し,法線ベクトル(面に垂直な単位ベクトル)をniとすると磁束は
Bが一定の場合Bとnのなす角をθとするとφ=(B・n)S=BScosθ
単位は,1[T]=1[N/A・m],1[N/Wb]=1[A/m],[BS]=T・m2=(N/A・m)×m2=N・m/A=Wb
レンツの法則
「誘導電流は,それの作る磁束がコイルを貫く磁束の変化を妨げる向きに生じる」
→ 右上図で磁石のN極を下にしてコイルに近づける場合(S極を遠ざける場合も同じ),コイルを電磁石と考えると上がN極下がS極になるように誘導電流が流れる(つまり磁石のNとコイル上面にできたN極が反発しあい,相対運動を妨げる)
例1 図のような磁界中で一巻きのコイルを下方にある速さで移動する場合,コイルにはどちら向きの誘導電流が流れるか。
解 NからSに向けて見て反時計まわり。
例2 図のように電磁石の先端に一巻きのコイルを配置した。
①スイッチを入れた直後,
②入れたままの時,
③スイッチを切った直後
の各場合についてコイルに流れる誘導電流の向きと,コイルがどちら向きに力を受けるかを答えよ。
解 ①スイッチを入れると右図のようにコイルを貫く磁束は左向きに増加する。レンツの法則によりコイルにはこの磁束
の増加を妨げる向きに太線矢印の向きに誘導電流が流れる。このため電磁石の左側がN極,コイルの右側も
N極になるので反発するので,コイルは左向きに力を受ける。
②では,コイルを貫く磁束は変化しないから,誘導電流が流れず,力を受けない。
③では①のN極とS極が反対になり,誘導電流の向きは反対だが,受ける力の向きは①と同じ。
例3 右図のように,断面積5.0×10-4[m2],巻き数500回のコイルが磁束密度の大きさ2.0[T]の磁界に垂直に置かれている。
磁束密度が一様に増加して,0.5[s]後に4.0[T]になった。このとき,ab間に生じる誘導起電力の大きさはいくらか。
またa,bいずれの電位が高いか。
解 誘導起電力の大きさをVとすると(20-1)式から
大きさは1.0[V]
誘導起電力は抵抗にb→aの向きに生じるので,bの方が電位が高い。
誘導起電力は一種の電池と考え,外部抵抗に対してどちら向きに電流を流すかで電位の高低を判断する。つまりこの場合コイルの下側が電池の正極,上が負極になったと考えられる。
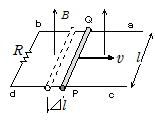
誘導起電力は磁界が時間に対して変化する場合だけ生じるだけではない。磁界が一定でも,導体が磁界中を移動する場合も誘導起電力は発生する。
磁束密度Bの一様な磁界中に,長さlの導線PQが2本の平行な導線ab,cdと両端を接して置かれている。この導線PQを一定の速さvで磁界と垂直の方向に横切って運動させる。誘導起電力の大きさは,微小時間⊿t 間に棒PQは
⊿l=v⊿t だけ移動するから,⊿t の間の磁束変化⊿φは
⊿φ=B⊿S=B(l・v⊿t)=Blv⊿t
よって生じる誘導起電力の大きさVは
(20-2)
閉回路bdPQを貫く磁束は棒PQが右方に移動することにより増加するから、レンツの法則よりPdbQの向きに誘導電流が流れるのでVP>VQである。
(Vの向きは速度vの向きからBの向きへ右ねじをまわし、ねじの進む向きである)
誘導起電力Vが生じたことにより,回路に誘導電流が流れるので,I が磁界 B から力 F を受ける。F の大きさは F=I l B=
で向きは左手の法則から図の左方、つまり運動を妨げる向きになる。一定の速度 v で移動させるため F と等しい外力 F ' を加え続けなければならない。一定の力F'を加えると,物体は等加速度運動するはずだが
この場合はF ' が一定だから v が一定になる。これは,F ' のする仕事率 P が
になることから,電気抵抗 R でのジュール熱として消費されていることになる。
上記のことをローレンツ力で考えると,以下の通りである。磁界Bの中でPQを図の向きに移動させるとPQの中の電子(電荷-e)はPからQに向かうローレンツ力 f=evBを受けるので,その結果としてQ端は電子が過剰になり負に帯電し,P端は正に帯電してP→Qの向きに電界が生じる。この電界の強さをEとすると定常状態では電子が電界から受ける力 eE とローレンツ力がつり合うので eE=evB よって,E=vB となる。PQ間の電界はどこでも同じだから,PQ間の電位差は
V=El=vBlとなり (20-2)と一致する。
したがってVP>VQ となって外部にはP→d→b→Qの向きに誘導電流を流すことになる。
電磁誘導は磁束の変化があれば,その空間にコイルがなくとも誘導起電力が発生することがその本質である。つまり,真空中であっても電磁誘導による電界が発生する。[20-1 電磁誘導の法則 例1] のコイルの代わりにアルミ板,銅板のように磁化しない金属板に変えたらどるだろうか。金属板を下に移動し,磁界に入り始めた場合,左図(×は磁界 B が紙面表から裏に向かうことを示す)にあるように金属板表面に電流が流れる(これを渦電流という)。20-3 自己誘導・相互誘導
渦電流の一番大きい部分は図で右向きであり,これが磁界Bから受ける力の向きは上向きであり,金属板の運動を妨げる向きに働く。金属板が磁界を出る場合も,同様にして金属板が磁界から出ることを妨げる向きに力が働く。この金属板を振り子状にして(右図)磁界に入れようとすると,上記と同様に金属板の運動を妨げる向きに電磁力が働き,電磁ブレーキとして使うことができる。
真空中で電子を一定半径の軌道で加速するための装置にベータトロンがある。半径rの円軌道の場合,誘導起電力Vは
で与えられ,この電界を利用して加速するのがベータトロンである。中心ほど強い磁界をかける必要がある。
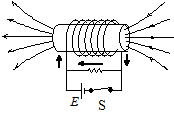
右図のように鉄芯入りコイルと電気抵抗,電池を配置する。
スイッチを入れた場合,抵抗に大きな電流が流れないが(抵抗の代わりに電球をつけると明るくない),その後スイッチを切ると一瞬大きな電流が抵抗に流れる。これは,流れている電流がすぐに止まらす,しばらくの間コイルと抵抗の間に電流が流れるためである。電磁誘導によって,コイルを貫く磁束が減少するのを妨げるためと考えると説明できる。スイッチを入れる場合より,切った場合の方がコイルを貫く磁束の変化が大きいためである。
このように,コイル自身に流れる電流変化によって誘導起電力(逆起電力ともいう)が発生する現象を自己誘導という。
自己インダクタンス(self-inductance)
コイルに発生する誘導起電力Vの大きさは右図のように,コイルに流れる電流I の時間変化に比例する。誘導起電力は(20-3)
で与えられる。ここにLは自己インダクタンスであり,コイルによって決まる量である。
Lの単位はH(ヘンリー)であり1H=1Vs/Aつまり,1[s]間に1[A]の電流変化があるときに1[V]の誘導起電力が発生する大きさである。
自己インダクタンスの例(ソレノイドの場合) 断面積S,透磁率μ,長さl,巻き数nとする。
φ=BS=(μ・n0I)S
コイルに蓄えられるエネルギー
コイルに電流を流すとコイルにはこれを妨げる向きに誘導起電力が発生することから,電池が電流を流すためにはこの誘導起電力に逆らって仕事をしなければならないことがわかる。
コイルに流す電流を0からI に増加させることを考える。電流I'を微小時間⊿tに⊿I'増加させるには,誘導起電力に逆らってコイルの両端にの電圧を加えなければならない。この間電流I'を流すために電源のした仕事⊿Wは電荷変化⊿q=I '⊿t だから
電流を0からIまで流すのに必要な仕事はLI-Iグラフの三角部分の面積で与えられる。
∴ コイルのエネルギーは(20-4) (
)
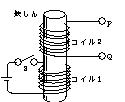
右図のようにコイル1,コイル2と同芯に巻く。コイル1に電池をつけ,スイッチを入れるとコイル1に誘導起電力が発生するだけでなく,コイル2にも同様に誘導起電力が発生する。このように,電気的に接続されない近接して置かれたコイルに起こるこのような現象を相互誘導という。
1次側コイルの電流をI1とすると,2次側コイルに生じる誘導起電力Vは(20-5)
で表される。負号は誘導起電力が1次コイルの電流の変化を妨げる向きに生じることを示す。比例定数Mを相互インダクタンス
(mutual inductance)という。単位は自己インダクタンスと同じH(ヘンリー)である。
例1 相互インダクタンスMの例
同芯に巻かれた1,2次コイル(それぞれの単位長当たりの巻き数n1,n2)の断面積をS[m2],長さを l [m]とする。
(20-3自己インダクタンスLと比べてみよ)
例2 図のように鉄心にコイル1,2を巻き,図に示すように抵抗値を変化させコイル1の電流を変化させた。
コイル2の誘導起電力の時間変化を描け。相互インダクタンスM=0.10Hとする。ただし,VP>VQの
場合を正とする。
解 0~2×10-2[s]:1次コイルに下向きに磁束が増加する。2次コイルにも下向きの磁束が増加するから誘
導起電力はPからQに向かう電流を流す向きだから,符号は正で大きさは
2~6×10-2[s]:磁束の時間変化がないから0
6~8×10-2[s]:0~2×10-2[s]の場合と符号が逆になるだけ。
ホーム メニュー 静電界 コンデンサー 直流回路 磁界 電磁誘導 交流