ホーム メニュー ![]() 序論・物理量 ベクトルとスカラー 落体の運動 力 運動の法則 円運動 仕事とエネルギー 運動量
序論・物理量 ベクトルとスカラー 落体の運動 力 運動の法則 円運動 仕事とエネルギー 運動量
【5】 落体の運動
ボールを重力のもとで投げ出すと一定の軌道を描くことは日常的に見られることである。
同時に,ボールを支えた手をそっと離すと,時間とともに速さを増すことが観察される。キャッチボールするときに,速く投げれば相手のミットに向けて投げればよさそうだが,はたしてそうだろうか。以下,特記のない限り次の仮定の下に落体の運動を考える。
①重力加速度g は一定とする。
②空気抵抗を無視する。
(1) 自由落下(初速度v0=0 の鉛直方向の落下運動) (freefall)
真空中で羽毛とボールを同時に自由落下させると,右上図のように全く同じ運動することがわかる。右図は空気中の自由落下のストロボ写真である。落体には重力しか働かないので,初速度v0=0,加速度a=g の一次元の等加速度運動である。
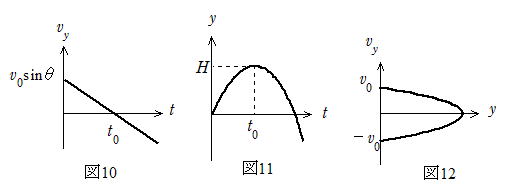
変位をy (鉛直下方を正の向きにとる),t=0でx0=0とすると,
速さと時間の関係
(4-7)式から v=v0+at → v=g t (5-1) (図①)
変位と時間の関係
(4-8) 式から  →
→ 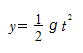 (5-2) (図②)
(5-2) (図②)
速度と変位の関係
(4-9)式から ![]() →
→ ![]() (5-3) (図③)
(5-3) (図③)

質問1 t [s] 後の速さは,t=1[s]の速さの何倍か。
( t 倍)
質問2 t [s] 後から1[s]間の落下距離は,はじめの1[s]間の落下距離の何倍か。
(2t+1)倍
質問3 y [m] 落下したときの速さは,はじめ1[m]落下したときの速さの何倍か。
(![]() 倍)
倍)
仮定について
注① 地球中心からの距離をr とすると,重力加速度g は,g ∝ (1/r2) であることが知られている(【8】円運動で学ぶ)が,地球の半径Rに対して小さい範囲において成り立つ。
注② 雨滴が落下する場合,ゴルフボールに回転をかけた場合など実際には無視できないが,①②の仮定があると,簡単な定式化が可能になる。このように,物理学に出てくる式は,どんな場合にも成り立つ「公式」ではない。与えられた式がどんな条件で成り立つかに十分注意しなければならない。
(2) 鉛直投射(鉛直方向に初速度v0を与えた落体運動)投げ上げ
鉛直上方を正の向きにとる。位置y,初速度v0,速度v,時刻tの間の関係式は次の通り。
v=v0- gt ・・・・(5-4) (図④)
![]() ・・・・・・・(5-5) (図⑤)
・・・・・・・(5-5) (図⑤)
![]() ・・・・・・・ (5-6) (図⑥)
・・・・・・・ (5-6) (図⑥)
最高点(v=0)までの所要時間t0は(5-4)=0から
![]()
最高点の高さHは(5-6)でv=0から ![]()
質問4 速度vが初速度のn倍になる時間は,最高点までの時間t0 の何倍か。
[(5-4)式から (1-n)倍]
質問5 速度vが初速度のn倍になる高さはHの何倍か。
[(5-6)式から(1-n2)倍]
投げ下ろし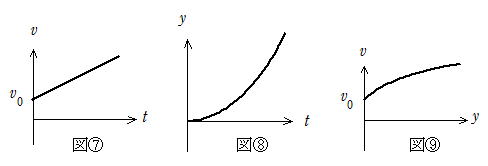
鉛直下方を正の向きにとる。位置y,初速度v0,速度v,時刻tの間の関係式は(5-4),(5-5),(5-6)式のg を正号に変えればよい。
v=v0+gt ・・・・(5-7) (図⑦)
・・・(5-8) (図⑧)
・・・・(5-9) (図⑨)
(3) 水平投射(水平方向に初速度v0を与えた落体運動)
初速度v0で水平投射された小球の水平方向に外力が働かないので,等速運動,鉛直方向には重力だけが働くので加速度g の等加速度運動である。
水平方向をx軸,鉛直方向をy軸(下方を正の向きにとる)とすると,投射されてからt [s]後の,座標をx,y,速度 vx,vy,加速度をax,ay とすると,以下の関係がある。
x方向
ax=0,vx=v0,x=v0・t ・・・・・・・(5-10)
y方向
ay=g,vy=gt,・・・・・・・(5-11)
x と y の関係式(軌跡の式)
x=v0・t,から t を消去して
・・・・・・・(5-12)
(4) 斜方投射(水平と角度θの向きに初速度v0を与えた落体運動)
初速度v0で水平と角度θで投射された小球の運動は,水平方向に外力が働かないから,v0cosθの等速運動,鉛直方向には重力だけが働くので加速度-g の等加速度運動である。
水平方向をx軸,鉛直方向をy軸(上方を正の向きにとる)とすると,投射されてからt[s]後の,座標をx,y,速度vx,vy,加速度をax,ayとすると,以下の関係がある。
x方向
ax=0,vx=v0cosθ,x=v0cosθ・t ・・・・・・・(5-13)
y方向
ay=-g,vy=v0sinθ-g t ・・・・(5-14) (図⑩)
・・・・・・・・・・・・・(5-15) (図⑪)
vy2-(v0sinθ)2=-2g y・・・・・・・(5-16) (図⑫)
x と yの関係式(軌跡の式)
(5-13),(5-15)式からt を消去して

参考 この式の包絡線はであることが知られている。
y軸方向のグラフ
質問6 最高点までの時間t0はいくらか。 (5-14)のvy=0から
質問7 最高点の高さHはいくらか。 (5-16)のvy=0から
質問8 水平到達距離Xはいくらか。 2t0を(5-13)に代入して
落下運動は,運動の対称性を考えると簡単になる場合がある。
■ 鉛直投射の最高点までの運動は,最高点から自由落下させた場合と対称
■ 斜方投射の最高点までの運動は,最高点から後半の運動と対称。最高点以降の運動は水平投射運動,
鉛直方向は,鉛直投げ上げ運動
■ 水平投射の鉛直方向の運動は,自由落下運動
モンキーハンティング(monkey hunting)
左図のように,原点にある物体Aを水平と角度θの延長線上にある物体Bに向けて初速度v0で投射すると同時に,物体Bを自由落下させると,必ずA,Bは衝突する。なぜか。
Aについて:軌跡の式の第1項はg の入ってない項で,物体Bのx座標が決 まればxtanθは物体Bの高さを示すことになる。第2項は
から書き直して出されたものである。
つまり,AはBの高さから自由落下したことと等価である。
Bについて:Bの高さから自由落下する。
よって,A,Bともに高さyが同じ値になるので必ず衝突する。
このとき,Bから見たAの相対速度はどのような値になるか。A,Bそれぞれの速度のx,y方向成分vAX, vAy,vBx,vByは vAX=v0cosθ,vAy=v0sinθ- gt ,vBx=0,vBy=-g t
x方向の相対速度は VX=vAX-vBX=v0cosθ
y方向の相対速度は Vy=vAy-vBy=(v0sinθ-gt)-(-gt)=v0sinθ
よってBから見たAの相対速度は(θ に関係してない)
つまり,つねにAはBに等速で同じ向きに近づいてくる。
(Aをハンター,Bをサルとしてこれをモンキーハンティングという。日本人はサルを鉄砲で撃ち落とす慣習はほとんどないと思うのだが)
上の問題で,BからもAに向けて同時に投射した場合,A,Bが衝突するか。
解 それぞれの初速度をvA,vBとする。また,Bのはじめのx座標をl,y座標をh,衝突点のx座標をl ' とする。
衝突するまでの時間tは
,lー l '=vBcosθt
∴
また,Bのy座標は
=h-(lー l ')tanθ-
=l 'tanθ-
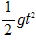
(∵ h-(lー l ')tanθ=l 'tanθ)
よって yA=yB
この結果,衝突点の高さyA(=yB) は初速度vA,vB に関係しない。
衝突の条件は互いに向かい合って同時に投射することである。
以下の各問で重力加速度gはg=9.8[m/s2]とし,空気抵抗は無視できるものとする。
5 落体の運動
問15 ある高さhから小球を自由落下させた。4.0(s)後に地面に落下した。hはいくらか。また,小球が地面に落下する直前の速さはいくらか。
問16 高さ19.6[m]のところから小球を自由落下させた。何(s)後に地面に達するか。その時の速さは何[m/s]か。
問17 高さ100[m]の塔から初速度19.6[m/s]で小球を投げ上げた。1.5[s]後の高さは何[m]か。
問18 小球を地面から真上に投射したら4.0[s]後に地面に落ちてきた。高さ14.7[m]の地点を通過するのは,投げ上げてから何[s]後か。
問19 図のように鉛直面内で,傾斜角がα の斜面上の一点Oからある質量の物体を投射角(水平面となす角)θ,初速度v0 で投げ上げた。水平方向 ,鉛直方向にx座標,y座標を図のように定める。ただし,0<α <90°とする。
(1) 投げ上げた時刻をt=0 として,投げ上げた後の時刻t における物体の位置x,yを求めよ。
(2) 斜面の位置を表す式を求めよ。
(3) 物体が斜面に到達した時刻を求めよ。
(4) Oから衝突点Pまでの距離lを求めよ。ただし必要があればつぎの公式を用いよ。
2sinθ1cosθ2=sin(θ1+θ2)+sin(θ1-θ2)
(5) 投げ上げ角θを変えて,斜面への到達距離OPを最大にするときの投げ上げ角をθmとして,角θmと傾斜角α の関係式を求めよ。また,このときの,OPの最大値lmを求めよ。
問20 1.8[m/s]の一定の速さで上昇する気球に乗った人が,鉛直上方に小石を投げたら,3.0[s] 後にすれ違って落ちていった。小石を投げるとき気球の速度は変化しないものとする。重力加速度の大きさを9.8[m/s2]とする。
(1) 小石に与えられた初速度はいくらか。
(2) すれ違うとき,気球から見た小石の相対速度はいくらか。
(3) 投げた位置は地上40[m]の高さであった。小石はすれ違ってから何[s]で地上に達するか。
問21 地上h の高さから球Aを自由落下させ,同時に地面から球Bを投げ上げたら,2球は中央の高さですれ違った。
(1) Bの初速度はいくらか。
(2) A,Bが地面に当たる時間差はどれだけか。
問22 打ち上げ花火が上昇中に破裂して散った小さな玉が,すべて等しい初速度v0で四方に飛び散るとしたら,その後これらの玉はどのように空中で分布するか。
ホーム メニュー 序論・物理量 ベクトルとスカラー 落体の運動 力 運動の法則 円運動 仕事とエネルギー 運動量
Top