(ウ)
(b) 原点は
波形である。0.1[s]は周期の1/4だからt =0の次の瞬間は-y方向に振動していることがわかる)
∴
問題解答 戻る
問93 (a)(ア) 波長λ=8.0[m](図より),
(イ) 0.9[s]が周期だから
T=0.9 ∴ T=0.4[s]
(ウ)[m/s]
(b) 原点はの単振動をしている。(∵ 1周期の2倍の時間0.8[s]が経過すると実線と同じ波形になり,それから0.9-0.8=0.1が破線の
波形である。0.1[s]は周期の1/4だからt =0の次の瞬間は-y方向に振動していることがわかる)
∴
問94 (a) ![]() (b)単振動 (c)
(b)単振動 (c) ![]() (d)
(d) ![]() (e) 定常波
(e) 定常波
①部分は定常波の振幅を,②は時間変動部分を示す。①部分が0ならば時刻tに関係なくy=0になるから
(g) 節 (h) 同様にして時刻t に無関係にy=2aになるのは
問95 13-1波動(4)から,音を横波とすると,その速さは![]() で表されるが,空気ではGの値が極めて小さいから,音速Vも小さくなるはず。また横波の場合粘性のためエネルギーが速やかに減衰し遠くまで達することはない。これらは事実に反する。音波の伝わる方向に平行に張った薄膜を置いても膜は振動しないが,直交するように置くと振動することからも縦波であることがわかる。
で表されるが,空気ではGの値が極めて小さいから,音速Vも小さくなるはず。また横波の場合粘性のためエネルギーが速やかに減衰し遠くまで達することはない。これらは事実に反する。音波の伝わる方向に平行に張った薄膜を置いても膜は振動しないが,直交するように置くと振動することからも縦波であることがわかる。
問96 (1) 波の振動数をf,波長を λとすると波の変位の式は
![]()
この式と与式を比べて,f =10Hz
(2) 図より入射波の波長λ は λ=8[m]だから,v=fλ=10×8=80[m/s]
(3) ある点の右側の媒質が左に動き,左側の媒質が右に動く点の密度は大きくなる。このような点はx=-5[m]である。また,媒質の速さが0になる点は変位の大きさが最大の場所だから,x=-7,-3[m]である。
問97 (1) λ (6行目・・・・壁に向かって垂直に進む音波の波長は,静止した人から見るとλである。つまり,進行方向で短くなった後の波長がλ )
(2) 音速と波長は比例するから
(3) 音源が静止しているときの波長をλ0とすると
反対側に出される音波の波長λ ' は
問98 (1) 位置xにおける波は原点から時間![]() かかって伝わるから,時刻tでの変位は原点での時刻
かかって伝わるから,時刻tでの変位は原点での時刻![]() における変位に等しい。
における変位に等しい。
∴ ![]()
(2) 重ね合わせの原理 (3)
(4) 固定端x=Lではy1(L,t)+y2(L,t)=0だから
y2(L,t)=-y1(L,t)=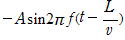
(5) π (6) x=Lからx までの距離はL-x だから,時間の遅れは
(7) y2(L,t)のtの代わりにに置き換えたものがy2(x,t)である。
(8)を用いると,合成波の変位は
(9) x=0を固定端とするとx=0で y(x,t)がt によらず常に0でなければならないから