ホーム  メニュー            波動    波の性質    音波   ドップラー効果  弦振動気柱振動    光波の諸性質    幾何光学
                                                                             

１４−２ ドップラー効果

一般に音源と観測者の間に相対運動があると，音源が静止しているときの振動数と異なる振動数の音を聞く。この現象をドップラー効果という。
1842年ドップラーによって発見された現象である。ドップラー効果は音の他に光(電磁波)の場合も起こり，天体の地球に対する相対速度の測定やスピード違反の速度測定にも使われている。
(1) 直線上の場合

�@ 音源移動，観測者静止の場合(波長が変化する)

右図のように音源Sが速さu(m/s)で観測者に近づく場合を考える。音速をV(m/s)，音源の振動数を f₀(Hz)，音源が静止しているときの波長をλ₀(m)とする。V＝f₀λ₀
1秒間で考えると，音源Sは1秒間にu(m)，音はV(m)進む。V−u(m)の間にf₀個の音が入っているから音源の進行方向の波長をλ (m)とすると
　　　V−u＝f₀λ     ∴  
よって，波長のずれはであり，見かけ上の振動数は      ･･･(a)
音源が観測者から遠ざかった場合は   である。

�A 音源静止，観測者移動の場合(波長は変化しない)

観測者が速さvで音源に近づく場合(右図)
観測者が静止していると，観測者を毎秒f₀個の音が通過し，音はV(m)進む。観測者が近づくと，毎秒v(m)の間に��f 個だけ多く音が通過することになる。波長は変化する理由がないので，観測者の聞く振動数をf とすると
      V＋v＝f λ₀       ∴    
振動数のずれは， である。
観測者が遠ざかる場合は  ･･･(b)    である。
�@�Aをまとめると，  
       ･････    (14-3)    ()である。
音源移動速度uは，音が観測者に近づく場合は負号，遠ざかる場合正号
観測者の移動速度vは，音が観測者に近づく場合正号，遠ざかる場合負号である。
(a)を書き換えると となる。
左辺は静止した観測者を通過する音の波長を示し，右辺は音源から見た場合の波長を示し，これらが等しいことが分かる。
(b)を書き換えると となる。
左辺は静止した観測者を通過する音の波長を示し，右辺は動く観測者を通過する波長を示し，これらが等しいことが分かる。

ドップラー効果は波源と観測者の相対運動で起こる現象だが，相対速度が等しくてもどちらが動くかによってみかけの振動数は異なる

直線上で，観測者が静止して音源が速さvで近づいた場合に観測者の聞く振動数f₁と，音源が静止していて観測者が音源に向かって速さvで近づいて聞く音の振動数f₂とすると，相対速度は互いにvで等しいのにf₁，f₂は等しくない。音速をV，音源の振動数をf₀とすると
               
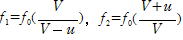
よって，観測者が静止して音源が速さvで近づいた場合の方が振動数が高い。

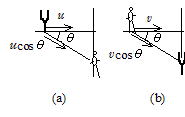
(2) 斜めの場合

右図のように音源の移動方向と観測者が直交する位置にいる場合，音源と観測者の移動速度のなす角度をθ とする。視速度(音源速度の観測者方向の成分ucosθ，観測者の音源方向の成分vcosθ)を(14-3)のu，vと置き換えると，観測者の聞く見かけ上の振動数は
  音源が移動する場合
          　　 (14-4)
   観測者が移動する場合
           (14-5-1)
角度θ と振動数の関係のグラフは右図。
θ＝0，π は直線上の場合と同じである。 

(3) 反射板がある場合

直線上に音源，観測者，反射板が右図のようにあるとする。反射板が動いてない場合，反射板は単に音の進む向きを変える働きをするだけだが，反射板が移動する場合は異なる。この場合は次のように考えればよい。
反射板の移動速度をw，音源，観測者の移動速度をそれぞれu，vとする。  
�@ 反射板が受け取る振動数f₁を求める(反射板を仮の観測者とする)。  
�A この音を反射板が発する音源とする。
�B 観測者が受け取る振動数を求める。      (14-5-2)

(4) 断続音の場合

断続音の間隔Tの逆数を仮の振動数とする。観測者が受け取る振動数f を求める。見かけ上の断続音の間隔は
1/fである。
断続音源が静止している観測者に速さuで近づいてくる場合，
          (14-5-3)

(5) 風が吹く場合

音の進む向きに風が吹く場合は音速を(V＋風の速さ)，逆向きの場合(V−風の速さ)として考えればいい。

(6) 円運動する音源の場合(観測者静止の場合)

視速度を(1)の(14-3)のuと置き換える。
速さvで等速円運動している音源があり，
�@ 観測者Pが円の外側にいる場合

視速度はvcosφで ，
音速をV，円の中心から観測者までの距離d，角度を右図のようにとると観測者の聞く振動数f は
                       (14-5-4)

�A 観測者Ｐが円の円周上にいる場合

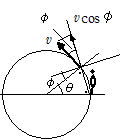視速度はvcosφ で，角度θ を右図のようにとると，φ＝θ/2だから，観測者の聞く振動数f は
         (14-5-5)

�B 観測者が円の内側にいる場合

運動の半径をa とし円の中心から距離b の位置に観測者がいる場合，右の角度をθ，α とすると，視速度はvsinα になる。図において正弦定理から

     

よって，見かけ上の振動数は
               (14-5-6) 

     が負の最大でfが最大 (sinθ1＝−1)
            ∴    
       が正の最大でfが最小 (sinθ2＝1)
              ∴  

ホーム  メニュー            波動    波の性質    音波   ドップラー効果  弦振動気柱振動    光波の諸性質    幾何光学
           Top