問題解答 戻る
問132
(1) 電源のした仕事が電子の運動エネルギーになるから
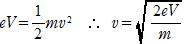 (m/s)
(m/s)
(2) (a) 負電荷を持つ電子がx 軸の正の向きに運動しているときにy軸の正の向きのローレンツ力をおよぼす磁場は,x 軸の負の向きの電流にy軸の正方向の電磁力をおよぼす磁場と同じ向きである。よって磁場の向きは,紙面表→裏(z軸の正)の向き。
(b) 電子の円運動の半径をr[m]とすると,向心力はローレンツ力evB[N]だから
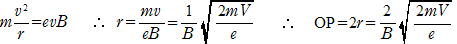 (m)
(m)
(3) (a) 電子は,磁場(z軸方向)に垂直方向にevBsin30゚[N]のローレンツ力を受ける。よって,z軸方向には速度vcos30゚[m/s]で等速度運動をし,
z軸に垂直方向には速さvsin30゚[m/s]の等速円運動をする。よって,電子はらせん運動する。
(b) z軸に垂直は等速円運動の半径をr '[m]とすると,
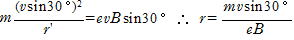 (m)
(m)
∴ 周期T=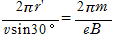 (s)
(s)
OQは,時間T[s]の間のz軸方向の移動距離だから
OQ=vcos30゚・T=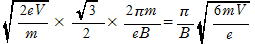 (m)
(m)
問133
(1) エネルギー保存則より
eV0=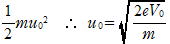
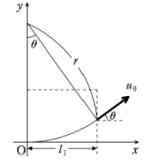
(2) 磁場(Ⅰ)を通過中に陽子は円運動を行う。その半径をr として
m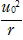 =eu0B ∴ r=
=eu0B ∴ r=
図より sinθ=
(3) 電場に入る陽子の速度のx,y成分u0x,u0yは
u0x=u0cosθ,u0y=u0sinθ である。
陽子は-y方向に電場からe の力を受けるから,陽子のy方向の加速度をaとして運動方程式を立てると
の力を受けるから,陽子のy方向の加速度をaとして運動方程式を立てると
ma=-e ∴ a=-
∴ a=-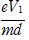
陽子はx方向に等速度運動をするから
wx=u0x=u0cosθ
また,陽子が電場の中を半分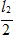 進む時間tは t=
進む時間tは t=
だから,速度のy成分wyは
wy=u0y+a t=u0sinθ-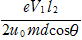
問134
(1) 電流が1.6×10-6Aだから,回路には毎秒1.6×10-6Cの電子が流れている。よって,1.6×10-6/1.6×10-19=1.0×1013個
(2) Aに対するBの電位が,-1.8V以上になると,Aから出た電子がBに到達するから,1.8eV 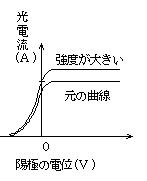
(3) 波長を変えずに強度を強くすると,飛び出す光電子の最大エネルギーは不変で,光電子の数が増える。
よって,右図のようになる。
(4) 振動数ν1,ν2の光を当てたときに出てくる光電子の最大運動エネルギーE1,E2はWを仕事関数,
hをプランク定数とすると次式で表される。
E1=hν1-W ……①
E2=hν2-W ……②
図3のグラフより仕事関数は,W=2.3eV
プランク定数は①,②よりWを消去して,h=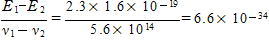 J・s
J・s
(5) このヘリウム・ネオンレーザーの振動数は,ν=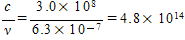 Hz
Hz
であり,電子の運動エネルギーが正になるために必要な最小の振動数は図3から5.6×1014Hzなのでこの値より小さいことがわかる。
したがって光電効果は起こらない。
問135
(1) [λ]=L,[p]=MLT-1,[h]=ML2T-1
(2) [λ]=[p]X[h]Y
∴ L=MXLXT-X・MYL2YT-Y=MX+Y・LX+2Y・T-X-Y
指数を比較して
L:1=X+2Y,M:0=X+Y,T:0=-X-Y
∴ X=-1,Y=1
(3) p= ,λ=
,λ=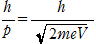 ∴ V=
∴ V=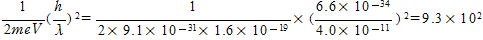 [V]
[V]
(4) 行路差=2dsinθ
回折の条件は 2dsinθ=nλ (n=1,2,3,・・)
(5) 右図より
sinθ=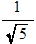 ,d=asinθ=
,d=asinθ=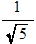 a
a
回折の条件は 2dsinθ= =nλ
=nλ
∴ n= =2倍
=2倍 
(6) (ⅰ) +y方向
(ⅱ) 右図よりsinθ= ,d=
,d= 
回折の条件:2dsinθ=2 ・
・ =a=nλ
=a=nλ
∴ n= =5倍
=5倍
問136
(1) 電子の速さを v とすると,X 線の最短波長λ0=3.5×10 -11m だから
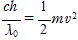 =eV ∴ V=
=eV ∴ V= (V)
(V)
(2) 電子が金属原子の核の近くを通過するとき,静電気力を受けて加速度運動を行い,エネルギーが減少して制動放射としてX線が放射される。
このエネルギー変化はさまざまな値をとるので,X 線のスペクトルは連続になる。
(3) ブラッグの条件 2dsinθ=nλ(n=1, 2, 3, ……) で n=4 の場合だから
d=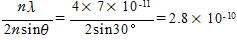 (m)
(m)
(4) eV= ∴ mv=
∴ mv=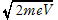 ∴ λe=
∴ λe=
(5) (4)から V=1 kVのときλe=3.9×10 -11 (m),V=2 kVのとき λe'=2.7×10 -11 (m)
ブラッグ反射条件から n =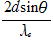 =7.2,n' =
=7.2,n' = =10.3
=10.3
よって,R が極大を示すのは n=8,9,10 の 3 回
問137
(1) 1.原子が光を放出することによってエネルギーを失い,消滅するはず。
2.原子が離散的な光を発することを説明できない。
(2) 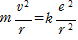 ∴
∴ 
(3) 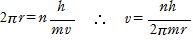 これと(2)から
これと(2)から 
(4) 
問138
 (1)(ア) 陽子 (イ) 中性子 (ウ) 質量数 (エ) α (オ) β (カ) γ (キ) -2 (ク) -4 (ケ) 1
(1)(ア) 陽子 (イ) 中性子 (ウ) 質量数 (エ) α (オ) β (カ) γ (キ) -2 (ク) -4 (ケ) 1
(2) 右図
(3) 1/2→5.0h, 1/8→15h
(4) 右図より,半減期Tは5.0hである。2T(=10h)後には
A=75(Bq)(A0/4),3T(=15h)後にはA=37.5(Bq)(A0/8)だから,A=A0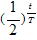
(5) A=kN,A0=kN0 (kは定数)と表せるから(4)の結果に代入して N=N0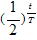
問139
(1)(ア) 原子番号 (イ) 質量数 (ウ) 放射性崩壊 (エ) 放射能 (オ) 放射性崩壊 (カ) ヘリウム原子核 (キ) 高速の電子(または電子)
(ク) 92 (ケ) 238-92=146 (コ) 92-2+1=91 (サ) 238-4=234 (シ) 同位体 (ス) 質量欠損
(2) 質量欠損⊿mは
⊿m={(390.29+1.67)-(154.28+232.34+3×1.67)}×10-27=0.33×10-27Kg
放出されるエネルギーは
⊿E=⊿m・c2=(0.33×10-27)×(3.0×108)2=3.0×10-11J
問140
(1) {(1.00866+10.01019)-(7.01435+4.00150)}×9.31×102=2.79=2.8[MeV]
(2) 反応後の ,
,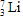 それぞれの運動エネルギーK1,K2は質量数に反比例するから
それぞれの運動エネルギーK1,K2は質量数に反比例するから
(K1/K2=7/4)
K1=2.79×( )=1.78,K2=2.79×(
)=1.78,K2=2.79×(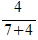 )=1.01
)=1.01
 :1.8[MeV],
:1.8[MeV],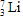 :1.0[MeV]
:1.0[MeV]
(3) ローレンツ力が向心力となる等速円運動する。電荷をq,質量をm,磁束密度をB,軌道半径をr とすると円運動の運動方程式は
m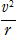 =qvB ∴ v=
=qvB ∴ v=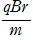
(2)から, ,
,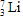 それぞれの速度,質量をv1,v2,m1,m2として
それぞれの速度,質量をv1,v2,m1,m2として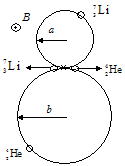
K1=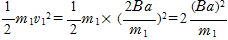
K2=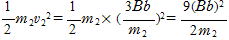
∴ 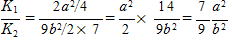
これと(1)から 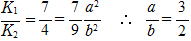 図は右図
図は右図
問141
(1)(ア) 質量数は(2+3)-1=4,原子番号は(1+1)-0=2 ∴ 
(2)(イ) 質量欠損
(3)(ウ) 特殊相対性 (エ) E=mc2
(4) ⊿E=⊿m・c2=0.019×1.66×10-27×(3.00×108)2=2.838×10-12≒2.84×10-12[J]
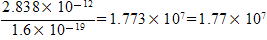 [eV]
[eV]
戻る





 (1)(ア) 陽子 (イ) 中性子 (ウ) 質量数 (エ) α (オ) β (カ) γ (キ) -2 (ク) -4 (ケ) 1
(1)(ア) 陽子 (イ) 中性子 (ウ) 質量数 (エ) α (オ) β (カ) γ (キ) -2 (ク) -4 (ケ) 1