(2) v一定のときは ma=-e E+kv=0 ∴ v=e E/k
(3) E=V/l,i=vSne から
問題解答 戻る
問110
(1) ma=-e E
(2) v一定のときは ma=-e E+kv=0 ∴ v=e E/k
(3) E=V/l,i=vSne から ![]()
問111
(1)(2) 対称性からab間とac間の電位差はそれぞれ等しい。したがってbc間に電流は流れない。よって抵抗R0に電流は流れないので,R0がなくても結果は同じである。 I0=0,Vbc=0
(3) 2RとRの直列接続で3Rになり,これが並列に2つ接続されているから
![]()
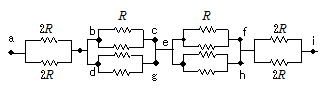
(4) それぞれが等電位になっている点は,b と d,c と e と g,f と h だから,等電位の点を図示して等価回路を考えるとつぎのようになる。
図2でbe間には抵抗値Rの抵抗が2個並列に入っており,de,ef,eh間も同じである。
よってRbe,=Rde=Ref=Reh=![]()
(5) 図3で考えるとすべての抵抗にの電流![]() が流れているので,ai 間の電位差は
が流れているので,ai 間の電位差は
![]()
問112
①電流計は内部抵抗小,電圧計は内部抵抗大にする必要がある。
②最大目盛りより大きい値を測定したい場合
電流計では外部抵抗を並列に
電圧計では外部抵抗を直列に接続する
電流計,電圧計は電気抵抗の直列並列接続の例と考えればよい
(1) 10[V]の電圧計にするためには,抵抗r ' を直列に接続する
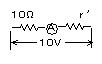 Imax=10×10-3=
Imax=10×10-3=![]()
∴ r '=1000-10=990=9.9×102[Ω]
100[mA]まで測定可能な電流計にするにはr ' を並列に接続する。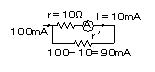
10×(10×10-3)=(90×10-3)r '
∴ r '=100/90=1.11=1.1[Ω]
(2) 電圧計rV=990+10=1.0×103[Ω]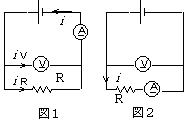
電流計 rV=![]() =1.0[Ω]
=1.0[Ω]
(3) 図1では i=iV+iR,V=iR・R ∴ R1=![]()
図2では V=i (R+rA) ∴ R2=![]() =R+rA >R
=R+rA >R
∴ R2>R>R1
問113
(1) 図のように電流の大きさ,向きをI1,I3,I4とすると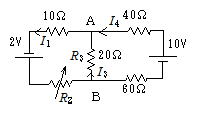
I1=I3+I4,2=I1(10+R2)+20I3
10=I4(40+60)-20I3
(2) R2=15[Ω]として(1)より
I1=0.088[A],I3=-0.01[A](図と逆向きに流れる),
I4=0.098[A]
また,VAB=20I3=0.2[V] (VA>VB),
R1:A→R1向きに0.088[A],
R4:R4→A 向き0.098[A],
R3:A→B向きに0.01[A]
(3) I3=0を(1)に代入して R2=10[Ω]
問114
問1 RLでの電力をP,電流をi とすると
![]()
よってRL=Rのときに最大値 ![]()
問2 ![]()
問3 右図のように電流I1,I2を定めると,キルヒホッフの法則から
E=I1R1+(I1+I2)R
両式から ![]()
I1R1=I2(R2+R), VRL=E/nより(題意)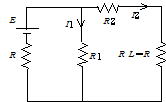
![]()
問4 最大電力になるのは R0=Rだから
![]()
これと問3から
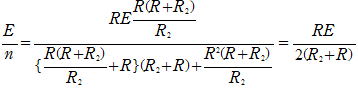
∴ ![]()